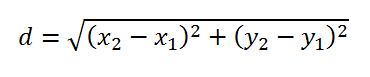LA CIRCUNFERENCIA

LA CIRCUNFERENCIA

Definición.- Es el lugar geométrico de todos los puntos que equidistan de un punto fijo llamado centro.

Circunferencia con centro en el origen.-

Circunferencia con centro (h,k).-

Ecuación general de una circunferencia.-

Si desarrollamos hasta su mínima expresión, obtenemos una ecuación de segundo grado en sus dos variables como los siguientes ejemplos:

• x² + y² + 5 x – 6 y + 6 = 0
•  x² + y² – x + 6 y – 8 = 0

Por lo tanto la ecuación general de una circunferencia es:

Elementos Notables de una Circunferencia:

Ver ejemplos:
ejemplos de circunferencias y sus ecuaciones


BIBLIOGRAFÍA:

• Serie Schaum - Geometría Analítica
• C. Lehman - Geometría Analítica
• F. Casazola - Matemática pre-universitaria

WEB GRAFÍA RECOMENDADA:

• http://www.vitutor.net/1/32.html
• http://www.aulafacil.com/matematicas-primero-eso/Curso/Lecc-40.htm
• http://www.ditutor.com/geometria/circunferencia.html

LA RECTA

LA RECTA

La recta es una sucesión infinita de puntos, los cuales tomados de dos en dos poseen la misma pendiente.

Una recta algebraicamente está representada por una ecuación de primer grado con dos variables, como los siguientes ejemplos:

•  3x -5 y +1= 0
• 2x – 7 y – 9 = 0
•  3x + 4 y - 1 = 0

Es decir, de manera general:

 Ax + By +C =0

 En pocas palabras, una ecuación de una recta tiene un término en "x", un término en "y" y un término independiente.

Maneras de determinar la ecuación de una recta:

DOS PUNTOS.- Si conocemos dos puntos de esta recta:

PUNTO – PENDIENTE.- Si conocemos un punto de la recta y su pendiente.

PENDIENTE – ORDENADA EN EL ORIGEN.-Si conocemos su pendiente y el punto de intersección de la recta con el eje de ordenadas.

ORDENADA – ABSCISA EN EL ORIGEN.- Si conocemos los puntos de intersección de la recta con los ejes cartesianos.

BIBLIOGRAFÍA.-

• Serie Schaum - Geometría Analítica.
• Algebra - Lazo.
• Sistemas Gráficos - Antonio Cuers , Sebastian Milán

WEB GRAFÍA RECOMENDADA.

• http://www.vitutor.com/geoanalitica.html
• http://www.vitutor.net/1/4.html

COORDENADAS CARTESIANAS

INTRODUCCIÓN A LA GEOMETRÍA ANALÍTICA

Geometría Analítica.- La geometría analítica es una rama de la matemática que estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.

Las dos cuestiones fundamentales de la geometría analítica son:

1.   Dado la curva en un sistema de coordenadas, obtener su ecuación.

2.   Dada la ecuación indeterminada, polinomio, o función determinar en un sistema de coordenadas la gráfica o curva algebraica de los puntos que verifican dicha ecuación.

Plano cartesiano.- Las coordenadas cartesianas o coordenadas rectangulares son un tipo de coordenadas ortogonales usadas enespacios euclídeos, para la representación gráfica de una función, en geometría analítica , o del movimiento o posiciónen física, caracterizadas porque usa como referencia ejes ortogonales entre sí que se cortan en un punto origen. Las coordenadas cartesianas se definen así como la distancia al origen de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes. La denominación de 'cartesiano' se introdujo en honor de René Descartes, quien lo utilizó de manera formal por primera vez.

Si el sistema en si es un sistema bidimensional, se denomina plano cartesiano. El punto de corte de las rectas se hace coincidir con el punto cero de las rectas y se conoce como origen del sistema. Al eje horizontal o de las abscisas se le asigna los números enteros de las equis ("x"); y al eje vertical o de las ordenadas se le asignan los números enteros de las yes ("y"). Al cortarse las dos rectas dividen al plano en cuatro regiones, estas zonas se conocen como cuadrantes:

·         Primer cuadrante "I": Región superior derecha

·         Segundo cuadrante "II": Región superior izquierda

·         Tercer cuadrante "III": Región inferior izquierda

·         Cuarto cuadrante "IV": Región inferior derecha

El plano cartesiano se utiliza para asignarle una ubicación a cualquier punto en el plano. En la gráfica se indica el punto +2 en las abscisas y +3 en las ordenadas. El conjunto (2 , 3) se denomina "par ordenado" y del mismo modo se pueden ubicar otros puntos.

Las coordenadas cartesianas se usaron un ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas se denominan abscisa y ordenada. La abscisa es la coordenada horizontal y se representa habitualmente por la letra x, mientras que la ordenada es la coordenada vertical y se representa por la y.

A continuación detallaremos algunas relaciones matemáticas que nos serán útiles en esta unidad:

Distancia entre dos puntos.-

 se calcula con la siguiente fórmula:

ver ejemplo:

Punto Medio.-

Angulo de Inclinación y Pendiente.- 

El ángulo de inclinación de una recta es el menor ángulo formado desde el eje de abscisas hacia la recta.

La pendiente "m" es la relación existente entre el cambio de posición vertical con el cambio de posición horizontal

Paralelismo y perpendicularidad.-

• Dos rectas son paralelas si sus pendientes son iguales.

• Dos rectas son perpendiculares si el producto de sus pendientes es -1

Angulo entre dos rectas.-

Sean las rectas L1 y L2 cuyas pendientes son m1 y m2, respectivamente, el menor ángulo formado desde L1 hasta L2, está en relación a sus pendientes, de la siguiente manera:

BIBLIOGRAFÍA:

• Serie Schaum - Geometría Analítica
• Andrés Armoran - Álgebra con geometría Analítica.

WEB GRAFÍA RECOMENDADA:

• http://www.sectormatematica.cl/contenidos/distancia.htm
• http://es.wikipedia.org/wiki/Geometr%C3%ADa_anal%C3%ADtica
• http://www.vitutor.com/geoanalitica.html