INTRODUCCIÓN A LA GEOMETRÍA ANALÍTICA
Geometría
Analítica.- La geometría analítica es una rama de la
matemática que estudia las figuras geométricas mediante
técnicas básicas del análisis matemático y
del álgebra en
un determinado sistema de coordenadas. Su
desarrollo histórico comienza con la geometría cartesiana,
continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y
más tarde con el desarrollo de la geometría algebraica.
Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las
matemáticas y la ingeniería, pues forma parte ahora del trabajo de
administradores para la planeación de estrategias y logística en la toma de
decisiones.
Las dos cuestiones fundamentales de
la geometría analítica son:
2. Dada la ecuación indeterminada, polinomio, o función determinar en un sistema
de coordenadas la gráfica o curva algebraica de los puntos que verifican
dicha ecuación.
Plano cartesiano.-
Las coordenadas cartesianas o coordenadas
rectangulares son un tipo de coordenadas ortogonales usadas
enespacios euclídeos, para
la representación gráfica de una función,
en geometría analítica ,
o del movimiento o posiciónen física,
caracterizadas porque usa como referencia ejes ortogonales entre
sí que se cortan en un punto origen. Las coordenadas cartesianas se definen así
como la distancia al origen de las proyecciones
ortogonales de un punto dado sobre cada uno de los ejes. La
denominación de 'cartesiano' se introdujo en honor de René Descartes, quien
lo utilizó de manera formal por primera vez.
Si el sistema en si es un
sistema bidimensional, se denomina plano
cartesiano. El punto de corte de las rectas se hace coincidir con el punto
cero de las rectas y se conoce como origen del sistema. Al eje horizontal o de
las abscisas se le asigna los números enteros de las equis ("x"); y
al eje vertical o de las ordenadas se le asignan los números enteros de las yes
("y"). Al cortarse las dos rectas dividen al plano en cuatro
regiones, estas zonas se conocen como cuadrantes:
·
Primer cuadrante "I": Región superior derecha
·
Segundo cuadrante "II": Región superior izquierda
·
Tercer cuadrante "III": Región inferior izquierda
·
Cuarto cuadrante "IV": Región inferior derecha
El plano cartesiano se utiliza para
asignarle una ubicación a cualquier punto en el plano. En la gráfica se indica
el punto +2 en las abscisas y +3 en las ordenadas. El conjunto (2 , 3) se
denomina "par ordenado" y del mismo
modo se pueden ubicar otros puntos.
Las coordenadas cartesianas se usaron
un ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya
sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres
ejes (en el espacio), perpendiculares
entre sí (plano y espacio), que se cortan en un punto llamado origen de
coordenadas. En el plano, las coordenadas cartesianas se denominan abscisa y ordenada. La abscisa es la coordenada
horizontal y se representa habitualmente por la letra x, mientras que la ordenada es la coordenada vertical y se representa por
la y.
A continuación detallaremos algunas relaciones matemáticas que
nos serán útiles en esta unidad:
Distancia entre dos puntos.-
Punto Medio.-
Angulo de Inclinación y Pendiente.-
El ángulo de inclinación de una recta es el menor ángulo formado desde el eje de abscisas hacia la recta.
La pendiente "m" es la relación existente entre el cambio de posición vertical con el cambio de posición horizontal
Paralelismo y perpendicularidad.-
- Dos rectas son paralelas si sus pendientes son iguales.
- Dos rectas son perpendiculares si el producto de sus pendientes es -1
Angulo entre dos rectas.-
Sean las rectas L1 y L2 cuyas pendientes son m1 y m2, respectivamente, el menor ángulo formado desde L1 hasta L2, está en relación a sus pendientes, de la siguiente manera:
- Serie Schaum - Geometría Analítica
- Andrés Armoran - Álgebra con geometría Analítica.


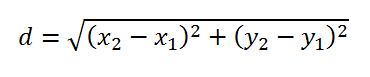



BUEN TRABAJO
ResponderEliminarVB yo estoy bien
ResponderEliminarCarlos quispe
ResponderEliminarMariel Violeta Navia Chambi
ResponderEliminarNicol Melani Chávez Coarite
ResponderEliminarFiorela chalco limachi
ResponderEliminarJose Armando Catari Chambi
ResponderEliminarViviana micaela Suarez corani
ResponderEliminarLeslie Tamara Quenaya Lliully
ResponderEliminarJhonatan Moisés Chuquimia Cortez
ResponderEliminarLiz Daniela Cusi Cornejo
ResponderEliminarimanol junior guarachi guarachi
ResponderEliminarSamuel cori chavez
ResponderEliminarSara Belen Chuquimia Mayta
ResponderEliminarDexter aliaga mamani
ResponderEliminarLiz Abigail Rodas Trujillo
ResponderEliminarLiz Abigail Rodas Trujillo
ResponderEliminarWendy Anahi Salas Calle
ResponderEliminarMarytte Dayan Flores Toledo
ResponderEliminarAlejandra quispe nava
ResponderEliminarRenny aguilar agno
ResponderEliminarMichelle Stephnie Miranda Miranda
ResponderEliminarMichelle Stephnie Miranda Miranda
ResponderEliminarNora Paucara Zuleta
ResponderEliminarRonald Luis Chejo Merlo
ResponderEliminarMiguel angel Sánchez escobar
ResponderEliminarKatherine Edith Cori Nina
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminar